Vol. 16 No. 2 January 2005
Modeling and Validating the Grabbing Forces of Hydraulic Log Grapples Used in Forest Operations
Jingxin Wang
West Virginia University
Morgantown, WV, USA
Chris B. LeDoux
USDA Forest Servic
Morgantown, WV, USA
Lihai Wang
Northeast Forestry University
Harbin, China
ABSTRACT
The grabbing forces of log grapples were modeled and analyzed mathematically under operating conditions when grabbing logs from compact log piles and from bunch-like log piles. The grabbing forces are closely related to the structural parameters of the grapple, the weight of the grapple, and the weight of the log grabbed. An operational model grapple was designed and tested to validate grabbing forces of the mathematical models while grabbing logs from five alternative diameter classes under two different working conditions. The working conditions and log sizes affected the grabbing forces significantly. Validation results suggest that the mathematical models developed can be used to estimate the grabbing forces required in the design process of log grapples. The results can be used by equipment manufacturers and researchers involved in the engineering design of grapples used in harvesting operations.
Keywords: Grabbing forces, log grapples, logging, forest operations, equipment manufacturing.
INTRODUCTION
Log grapples are mechanisms for handling timber, which can be attached to crane systems, knuckle-boom loaders, grapple skidders, forwarders, or other machines for loading, unloading, sorting, and stacking operations either in log yards or on logging sites. A grapple can be classified as either a radial or an axial grapple depending on its holding position of the logs. Radial grapples are widely used and can be further classified into electrically driven or hydraulically driven based on the power source used. The hydraulically driven grapples are the most popular models and can be grouped into inclined cylinder, vertical cylinder, and horizontal cylinder grapples based on the cylinder's position [11].
The theoretical aspects of grapples that must be considered during the design process are the forces that act on the grapple, structural properties, parameters and kinematics of the grapple [10]. Since 1950, several methods have been applied to analyzing and computing the grabbing resistance or grabbing forces of log grapples. The design concepts and the grabbing resistance of log grapples were first introduced and described by Taybep [6]. The tension force of electric hoists was described for grapples using the energy method [4]. The energy method calculates the grabbing resistance from the energy consumption point of view, that is, the work done by the external force should be equal to the energy consumed by moving the logs or the displacement work of the log grapple according to the laws of energy conservation [6, 10]. The displacement of a log grapple component, however, is very difficult to measure in the grabbing process using the energy method. Therefore, it is hard to use this method to determine the grabbing resistance accurately. The grabbing resistance of grapples was also calculated based on the friction forces among the logs [7]. This approach considered only the log movements regardless of the structure of the grapple. The direction and acted point of grabbing resistance could not be determined by this approach. The patterns of log movement also varied greatly with working conditions. The grabbing resistance force could be calculated based on the lever equilibrium principle [3]. The advantage of this method is that the value and direction of the force could be determined graphically. This method, however, might result in a certain error and would be impossible to use if there are more than two unknown variables in the model. The forces acting on the tongs of a log grapple could be assumed with a certain distribution, which was then used to determine the grabbing forces []. The main problem with this approach is how to determine the distribution pattern. A literature review of log grapples described the basic conditions and development of log grapples in forest operations [9, 11].
Many applications of the use of log grapples can be found in Scandinavian and North American forest operations, especially grapples used as attachments to skidders. The use of grapple skidders in conjunction with shovel logging has been shown to reduce soil disturbance and road building costs [1]. Kleunder and Stokes [2] reported that grapple skidders had consistently higher volumes and lower times per cycle when compared to cable skidders.
Grapple skidders have been used extensively in the Southern U.S. for many years to form a harvesting system configuration that along with feller-bunchers has shown to have utilization rates of up to 75 percent [8]. However, only a few references could be obtained about the design or mechanics of log grapples. Since the grabbing force is the key factor that is used to determine the structure and parameters of a grapple during the design process, it is essential to develop better models in order to understand the grabbing forces involved. Accordingly, in this research we (1) developed a new mathematical model for estimating grapple resistance forces, (2) validated it by comparing the mathematical results with actual operational measurements, and (3) used the mathematical model to illustrate the relationships between the grabbing force and the working conditions and log size.
MODELLING GRABBING FORCES
Knuckle-boom loaders and forwarders use their self-contained log grapples to load logs onto tractor-trailers or unload logs from trucks onto the deck while grapple skidders usually grabbed tree bunches and extracted them from the woods to the landing. The ways that the logs are grabbed can be categorized into the following working conditions:
The grabbing force is the force exerted on the tong and is used to close the tongs of the grapple. Grabbing resistance is the reaction force of the grabbing force. In order to model the grabbing force, the grabbing resistance must be identified first. Three assumptions were made about the grabbing resistance forces acting on the tongs of the grapple while grabbing:
Model For Grabbing Compact Log Piles
When the grapple starts to grab the logs, the tongs' tips are first placed in the gap between logs. Then the grapple's tongs are gradually closed. Since the grapple is symmetric in structure, the forces acted on the log grapple can be described as shown in Figure 1a. The resistance distribution on the external face of the tong is discrete and usually does not follow a pattern and varies depending on the method of grabbing. Therefore, the resultant force is used to represent this resistance in the model.
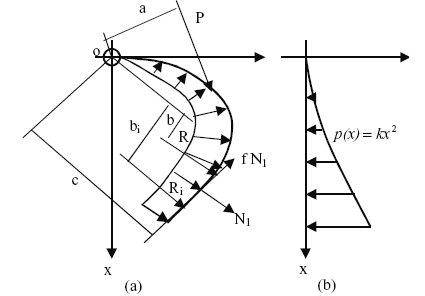
Figure 1. Diagram of the forces acting on the tong of the grapple.
If we let R be the resultant force of ΣRi, then the moment around point o for the grapple at its equilibrium state can be expressed as:
(1)
where, P = the grabbing force (Newtons);
Ri =
ith component of the grabbing resistance;
a, c, bi = the positions of forces related to
the structure of the grapple;
f = the friction coefficient between the logs
and the tong of the grapple;
N1 = the normal pressure of the grapple
exerted on the outside the tongs;
If the resultant force R is substituted for ΣRi in equation (1), a coefficient k1 must be used for adjusting the difference between the assumed resultant resistance and the actual resistance and k1 takes a value between 1.0 and 1.3 [12]. To simplify the modeling process, it is not necessary to leave mo(N1) in equation (1) since it will enhance the grabbing force. Hence,
(2)
If we let mo(R) (the moment of forces around point o) represent R´b (b is the vertical distance of R to point o), equation (2) can be expressed as,
(3)
Therefore, the grabbing force P acting on the tong of the grapple is expressed as:
(4)
where, a, c, f are known and mo(R) and N1 need to be determined.
Calculating mo(R)
In Figure 2, X1OY1 is a fixed coordinate and the coordinate of XOY moves with the tong's movement. If we let WG be the weight of the grapple in Kg, WL be the weight of the grabbed logs in Kg, R be the resultant force of grabbing resistance in Newtons (N), Hf, Vf be the internal forces in the tong's joint (N), a be the angle between axes X and X1, and b be the angle between axis X and the tangent line of acting point of R; then the moment around joint o can be expressed as:
mo (R) = mo (F) + mo (N2 ) (5)
The mo(N2) and mo(F) are then expressed as,
(6)
(7)
If we substitute mo(F) and mo(N2) in equation (5) into equations (6) and (7), we have,
(8)
Then in order to determine N2, F and N2 need to be reflected and resolved on the axes X1 and Y1. Then, we can solve for Rx1 and Ry1 as follows:
(9)
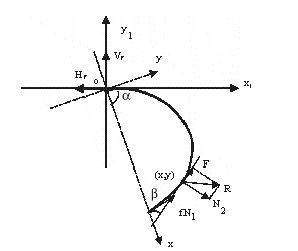
Figure 2. Model diagram of the grabbing resistance.
The grapple is assumed to hold the total weight of grabbed logs when the grapple's tongs are closed and the tips of tongs are juxtaposed. Under such a working condition, Ry1 acting on a tong of the grapple can be expressed as:
(10)
where, k2 = coefficient of the unbalanced load in the grapple (k2 = 1.0 to 1.2) [10];
g = acceleration of gravity (9.8 m/s2);
Therefore,
(11)
Then if we let
(12)
Substituting N2 in equation (8) into equation (12), we have,
(13)
Calculating the Value, Acting Direction and Point of R
From equation (9), we can express R as follows:
(14)
Therefore,
(15)
If we let q represent the acting direction of R and q be the angle between R and axis X1, then we can solve the tgq as follows:
(16)
The acting point of R on the tong can be determined based on the distribution of grabbing resistances along the tong. If we let xp denote the vertical distance from the acting point to the joint of the grapple and h be the distance between the joint and tip of the grapple (Figure 3), we have,
For (the grabbing of a log pile), we can solve for xp as follows:
(17)
Then k can be calculated as follows:
(18)
For (the grabbing of a log bundle),
(19)
Figure 3. Diagrams of the acting points and directions of the grabbing resistances.
Similarly, k can be calculated by the following expression,
(20)
Once we solve for xp, the acting point of R can be determined, which is point C (Figure 3). Then, g becomes the angle between N2 and R, which computed as follows:
(21)
Calculating N1
When the grapple completes the grabbing and the tongs are closed, the following equation is always true.
(22)
Where, the angle of 150 is the angle between the line segment along the tong's tip section and the horizontal line. Substituting equations (13) and (22) into equation (4), we have,
(23)
Then if we let ; equation (23) can be simplified as:
(24)
Since angles of a + b + y and a + b + j could be greater than 180°, the absolute values of sin(a + b + y) and sin(a + b + j) must be used in equations (24) and (25).
Model For Grabbing A Log Bundle
If the grapple grabs the log bundle, fN1c = 0 in equation (4). Therefore,
(25)
In a practical application, a and b are known and a is between 0 and 900 and can be expressed as:
(26)
where, d = the distance between two tips of the grapple's tongs (d is between 0 and the tongs maximum spread);
c = the distance between the tip of tong and the joint of grapple.
Then if the curve function of the grapple's tong is known, say y = f(x), then b can be obtained as follows:
(27)
MODEL VALIDATION TESTS
An operational log grapple was designed and tested in the Mechanical Lab at the Northeast Forestry University, Harbin, China (Figure 4). Two inclined hydraulic cylinders were used for opening and closing the tongs of the grapple and two 3-ton pulling/pressing sensors were attached to the end of each cylinder for recording the grabbing forces. An additional cylinder was also adopted for lifting the grapple. The technical parameters of the grapple are listed in Table 1. The pulling/pressing sensors were calibrated on the material testing machine and the linear relationship between the load and fluctuation height was obtained by using the least square method.
Table 1. Parameters of the grapple used in the tests.

l = kbh (28)
where l = load in N;
h = height of the calibration curve under a specific load;
kb = coefficient of calibration; kb can be computed based on the following equation.
(29)
where, hi = ith height of the calibration curve under load li;
li = ith load;
n = the number of times loads were summed during calibration;
kb = constants 204.2 N/mm and 367.5 N/mm respectively for the sensors we calibrated.
The logs grabbed during the tests were grouped into 4, 8, 12, 16, and 20 cm scaling diameters and were 2 m in length. The species used included Siberian spruce, birch, and other pines. A total sample of 15 logs was tested for each diameter class. Since logs were labeled at the ends, their positions in the log piles were the same before each test. Two working conditions were also simulated for each diameter class.
Figure 4. Diagram of the structure of the grapple tested.
Three variables were measured for each experiment - grabbing force 1, grabbing force 2, and the grabbed log weight. The two sensors attached between the grabbing cylinders and the tongs of the log grapple measured the grabbing force 1 and 2 respectively. A total of 150 experiments were conducted to measure the weight of the grabbed logs and the grabbing forces. An analysis of variance (ANOVA) model was used to determine if differences existed in the weight of the grabbed logs and the grabbing forces. The ANOVA model can be stated as follows:
(30)
Where Fijk represents the kth observation of the grabbing force or the grabbed log weight under the ith working condition and the jth log diameter treatment, m is the mean of each response variable, wi is the effect of ith working condition, dj is the effect of jth log diameter, eijk is an error component that represents all uncontrolled variability, and n is the number of observations within each treatment. The grabbed log weights averaged 164.7 and 180.9 Kg for grabbing the compact piles and the log bundles respectively and differed significantly (F = 109.88; df = 1, 149; P = 0.0001) (Table 2).
There is a significant difference among the grabbed log weights across diameter classes (F = 427.47; df = 4, 149; P = 0.0001) and ranged from 131.1 Kg for 4 cm logs to 215.0 Kg for 20 cm logs. The grabbing force 1 was significantly different between working conditions (F = 116.28; df = 1, 149; P = 0.0001). On average 9545.2 N was needed to close the tongs and grab the logs on compact piles and 7872.0.3 N to grab the log bundles. The grabbing force 1 was between 6997.1 N and 10420.3 N for grabbing logs of 4 to 20 cm in scaling diameter and was significantly different among diameter classes (F = 63.94; df = 4, 149; P = 0.0001). Similarly, there is also a significant difference of the grabbing force 2 between working conditions (F = 38.85; df = 1, 149; P = 0.0001) with an average of 8293.0 N for grabbing compact piles and 7320.9 N for grabbing the log bundles. Grabbing force 2 varied from 6262.8 N when grabbing 4-cm logs to 9006.6 N when grabbing 20-cm logs. Grabbing force 2 was not significantly different between 8 and 12 cm, 16 and 20 cm diameter classes. If grabbing force 1 and grabbing force 2 were averaged, the average grabbing force was also significantly different between working conditions with 8919.1 N for the grabbing of compact log piles and 7596.4 N for the grabbing of log bundles (F = 88.80; df = 1, 149; P = 0.0001). The average grabbing force was between 6630.0 N and 9713.4 N when grabbing logs of 4 to 20 cm. There was no significant difference when grabbing logs between 16 and 20 cm in scaling diameter. The unit grabbing force was also measured by the ratio of the average grabbing force and the grabbed log weight. There was a significant difference between grabbing compact log piles and log bundles with the average of 55.3 and 42.0 N/Kg respectively (F = 191.01; df = 1,149; P = 0.0001). However, the unit grabbing force did not differed significantly among diameter classes of 4, 8, and 12 as well as between logs of 16- and 20-cm in diameter.
Table 2. Means and significance levels of statistics for the log grapple during tests1.
| Work conditions | Diameter (cm) | ||||||
|---|---|---|---|---|---|---|---|
| Compact | Bundle | 4 | 8 | 12 | 16 | 20 | |
| Grabbed log weight (Kg) | 164.7a | 180.9b | 131.1c | 152.7d | 160.2e | 205.1f | 215.0g |
| Grabbing force 1 (N) | 9545.2a | 7872.0b | 6997.1c | 7852.3d | 8529.0e | 9744.2f | 10420.3g |
| Grabbing force 2 (N) | 8293.0a | 7320.9a | 6262.8c | 7317.7d | 7631.7d | 8816.1e | 9006.6e |
| Average grabbing force2 (N) | 8919.1a | 7596.4b | 6630.0c | 7585.0d | 8080.4e | 9280.1f | 9713.4f |
| Unit grabbing force (N/Kg)3 | 55.3a | 42.0b | 50.9c | 49.9c | 51.3c | 45.4d | 45.7d |
1Means with the same letter in a row are not significantly different at the 5 percent level with Duncan's Multiple-Range Test.
2The average of grabbing force 1 and grabbing force 2.
3The ratio of average grabbing force and grabbed log weight.
The models for the grabbing forces were validated by comparing the calculated mean grabbing forces achieved by the mathematical models with the means of the measured grabbing forces under the two different working conditions (Table 3). The grabbing forces were calculated by equation (24) for grabbing compact log piles and by equation (25) for grabbing log bundles. When the tongs of the operational grapple being tested were closed and the tong's tips were juxtaposed, the parameters used in equations (24) and (25) were assigned as follows:
α = 14.860 +
900 = 104.860 = 1.83 radian
ß = 390 =
0.68 radian
x = 42 cm
y = 13 cm
a = 13 cm
c = 48 cm
k1 = 1.1
k2 =1.15
f = 0.5
The mean of the grabbed log weights under each combination of working condition and diameter class was also used for input to compute the grabbing force. The average grabbing forces of operational variables for grabbing force 1 and grabbing force 2 was comparable.
The difference between calculated and measured grabbing forces never exceeded 11 percent for grabbing compact log piles and never exceeded 10 percent for grabbing log bundles (Table 3). Generally speaking, the differences of the grabbing forces for grabbing compact log piles was higher than those for grabbing log bundles. For example, the difference in grabbing logs of 16cm in a compact pile was over 10.2 percent while it was only 5.3 percent for grabbing log bundles. This is because the grabbing of a compact log pile was a more complicated situation compared to grabbing log bundles and the grabbing force was affected not only by the logs being grabbed but also from the forces of the logs underneath the log grapple. Based on the validation test comparisons we concluded that the models could be used to estimate the grabbing forces of the grapple.
DISCUSSION AND CONCLUSIONS
The grabbing forces of hydraulic grapples are closely related to the grabbing capacity, the weight, the structural parameters of the grapple, and the grabbed log/bundle weight. The mathematical models developed can be used to estimate not only the grabbing forces, but also the magnitude, acting direction and grabbing resistance on the tong of the grapple under working conditions of grabbing a compact log pile or a log bundle.
Validation tests indicated that the grabbing resistance or grabbing force was significantly affected by log size in terms of diameter class and working condition. Grabbing log bundles is easier than grabbing logs from compact piles. The grabbing forces needed for grabbing compact log piles were about 15% more than the force needed for grabbing log bundles. The grabbing resistance increased as the log size increased. Correspondingly, the average grabbing force increased about 46% from 6630.0 N when grabbing 4-cm logs to 9713.4 N when grabbing 20-cm logs. However, if the logs are extremely large, the grapple may only be able to handle a single log per grab. Under such situations, the grabbing force needed is only to hold the one log. The unit grabbing forces generally decreased with the log size and decreased about 10% from 50.9 to 45.7 N/Kg.
Table 3. Comparisons of the grabbing forces between calculated and measured forces.
| Working conditions | Scaling diameter (cm) | Grabbed log weight (Kg) | Calculated grabbing force (N) | Measured average grabbing force (N) | Difference (%) |
|---|---|---|---|---|---|
| 4 | 125.9 | 7237.1 | 7460.5 | -3.1 | |
| 8 | 146.7 | 8253.4 | 8434.2 | -2.2 | |
| Compact | 12 | 149.7 | 8400.0 | 9115.0 | -3.4 |
| 16 | 198.5 | 10784.4 | 9685.5 | +10.2 | |
| 20 | 202.8 | 10994.5 | 9900.6 | +9.9 | |
| 4 | 136.3 | 5438.7 | 5799.5 | -6.6 | |
| 8 | 158.8 | 6270.8 | 6735.9 | -7.4 | |
| Bundle | 12 | 170.8 | 6800.3 | 7045.7 | -3.6 |
| 16 | 211.7 | 8428.8 | 8874.7 | -5.3 | |
| 20 | 227.1 | 9041.9 | 9526.5 | -5.4 | |
Since the grabbed log weight is the only parameter in the mathematical models that comes from the logs being grabbed, the models developed could not directly identify the relationship between the grabbing resistance/force and log diameter or other characteristics. The difference between calculated grabbing forces and the measured average grabbing forces for grabbing compact log piles was higher compared to grabbing log bundles. This suggests that other factors such as inertia resistance due to the logs' movement should be considered in future models. However, the difference for grabbing log bundles was between -7.4 and -3.6 percent and the calculated grabbing forces were consistently lower than the measured forces. This is because the friction resistance between the outside face of tongs and the ground and/or other objects might exist and needs to be considered. Therefore, a coefficient of 1.1 needs to be added to the models to adjust the grabbing forces so that the model predictions line up with the experimental observations. Log movements and the friction resistance between logs should be explored during grabbing in the future studies. Further tests might be needed to examine how the structure of the log grapple and the logs from larger diameter classes affect the grabbing forces.
The validation test comparisons showed small differences between the mathematical and the operational results. Based on these results we concluded that the mathematical models can be used to estimate grabbing forces for grabbing logs from compact piles and from log bundles typically encountered in most logging operations. A spreadsheet program is available to users upon request from the authors that simplifies the calculations.
AUTHOR CONTACT
Prof. Jingxin Wang can be reached by email at --
jxwang@wvu.edu
REFERENCES
[1] Egan, A. F. 1999. Residual stand damage after shovel logging and conventional ground skidding in an Appalachian hardwood stand. Forest Products Journal. 49(6): 88-92.
[2] Kleunder, R. A. and B. J. Stokes. 1994. Productivity and costs of three harvesting methods. Southern J. of Applied Forestry. 18(4): 168-174.
[3] Li, K. and Y. Zhu. 1979. Calculation of the grabbing force of the log grapple under certain working condition. Forestry Research and Design. No. 2. [In Chinese].
[4] Shen, X. 1983. How to determine the power of the electrical hoist used on log grapple. Forest Logging Science, No. 2. [In Chinese].
[5] Shi, J. 1981. Design of log grapple for unloading trees-length. J. of Northeast Forestry University. 9(3):45-54. [In Chinese].
[6] Taybep, B. A. 1957. Kinematics of the grabbing mechanism. Forest Machinery Institute of Moscow, Publication No. 7, Moscow, Russia.
[7] Taybep, B. A. 1960. The grabbing mechanism. Forest Machinery Institute of Moscow. Moscow, Russia.
[8] Thompson, J. D. 2001. Calculating utilization rates for rubber-tired grapple skidders in the Southern United States. Proceedings of the 24th Annual COFE Meeting. Snowshoe, West Virginia. July 18-19, 2001: pp. 29-31.
[9] Wang, J. 1989. Basic conditions and developments of log grapple used both in China and abroad. Forest Logging Science. No. 4: 39-48. [In Chinese].
[10] Wang, J. 1990. Study on the theories of log grapples. Ph.D. Dissertation. Northeast Forestry University, Harbin, China. 311 pp.
[11] Wang, J. and G. Li. 1993. A review of log grapple used in China. J. of Forest Engineering. 4(2): 33-36.
[12] Wang, Z. and Z. Fan. 1985. Design and calculation of the log grapple. Forestry Machinery. No. 3: 23-30. [In Chinese].
The authors are, respectively, Assistant Professor, Division of Forestry, West Virginia University, Project Leader, Northeastern Research Station, USDA Forest Service, and Professor, College of Engineering and Technology, Northeast Forestry University.