 (1)
(1)Vol. 13 No. 1 January 2002
Jingxin Wang
West Virginia University
Morgantown, WV USA
The author is an Assistant Professor, Division of Forestry, West Virginia University.
ABSTRACT
Three log grapple tong shapes used in logging operations; horizontal ellipse, circle, and vertical ellipse, were analyzed mathematically and mechanically. The three same tongs as defined were designed and tested to evaluate their performance in terms of grabbing unrestrained log piles. Three operational variables; grabbing force, grabbed log weight, and unit grabbing force were examined using five diameter classes of logs for each set of tongs. Results indicated that the grabbing performance of log grapples with horizontal ellipse tongs is better than the grapples with circular tongs or vertical ellipse tongs.
Keywords: Tong shape, log grapple, log yard, logging, forest operations.
INTRODUCTION
A log grapple is a typical grabbing mechanism attached to the crane system for loading and unloading operations in log yard. The tong is a major component of a log grapple. When tongs of a log grapple are closed and their tips are juxtaposed, their internal surface outline is generally defined as the tong shape. Since the shape of a tong can affect grabbing resistance, tongs closed area, and grabbing capacity, the evaluation of the effects of tong shapes on log grapple's performance has been becoming a concern to researchers and designers of log grapples. Studies on the tong shapes of log grapples are very limited. Taybep [4] investigated the effect of shovel shape on its performance using kinematics. The shovel shape did have effects on its holding capacity for handling construction materials in the harbor [1, 6]. Fan et al. [3] analyzed stress distribution along the grapple's tongs using a photo-elastic method based on a plastic grapple model. They found that the performance of vertical ellipse grapple was better than others with respect to stress distribution. The effect of tong shape on the performance of a log grapple was analyzed mathematically [2]. Basically, it assumed that the tongs of a grapple were not movable and the log was rotating upward along the tong. This assumption was not realistic and is questionable in practical applications. In reality, the tongs are being closed gradually while grabbing logs. Grabbed logs are not being rotated upward along the tongs and falling into the holding area of log grapple. The grapple actually grabs logs in a digging way.
The objectives of this study are to (1) compute the grabbing resistance of log grapples comparing three different shapes of tongs under actual working conditions of grabbing unrestrained log piles, (2) test and measure the grabbing forces of log grapples with these three sets of tongs, and (3) compare and evaluate the effects of tong shapes on the performance of log grapples.
MATHEMATICAL EQUATIONS OF TONG SHAPES
Many shapes of tongs have been used in the log grapples for loading, unloading, sorting, and stacking operations. The shapes of these tongs, however, can be categorized into three basic groups: approximately horizontal ellipse, circle, and vertical ellipse tongs (Figure 1). In order to compare these three different shapes of tongs, the tongs closed area and open tongs maximum spread for them must be the same. Under such situations, the equations which describe the shapes of three sets of tongs can be expressed as follows:
(a)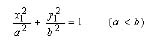 (1)
(1)
(b)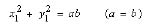 (2)
(2)
(c)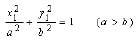 (3)
(3)
The joint of tongs is usually located on the top part of tongs at point o as shown in Figure 1. If y1 axis is translated to y-axis, a new coordinate of xoy is set. The mathematical equations (1), (2) and (3) can then be expressed in the coordinate of xoy.
For a horizontal ellipse,
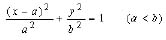 (4)
(4)
In order to compare the grabbing resistance, Equation (4) needs to be differentiated. If differentiate Equation (4) on both sides, we can have,
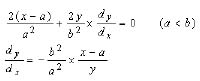 (5)
(5)
If let x - a = ρ cosθ, y =
ρ sinθ, Equation
(5) can be expressed as,
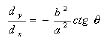 (6)
(6)
Where, ρ = polar radius
θ = polar angle
Similarly, for a circular tong,
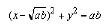 (7)
(7)
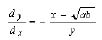 (8)
(8)
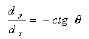 (9)
(9)
For a vertical ellipse,
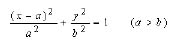 (10)
(10)
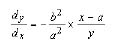 (11)
(11)
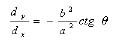 (12)
(12)
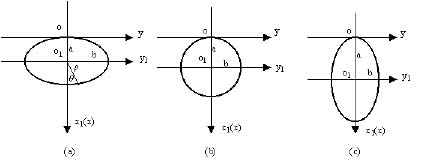
Figure 1. Basic tong shapes of log grapple.
GRABBING RESISTANCE
The grabbing resistance between the tongs of a log grapple and the logs differs due to the different shapes of tongs. In order to compare the relative grabbing resistance among three tong sets, a grabbing resistance force model should be developed considering the shape factors of the tongs. In Figure 2a, assume that the xoy coordinate is movable with the tong and x1oy1 is a fixed coordinate system. There are two free bodies: log and tong in the mechanics model of grabbing logs. While grabbing a log or a bundle of logs, the following forces are exerted on the tong: (1) the contact force from logs at contact point (x, y), which includes the forces generated by the weight of the log (Lwg) and the pressure resultant (Pl) transferred from other logs, (2) the force at pivot point o including the internal force at pin (Fo) and half of the weight of grapple (Gw) and grabbed logs (θ), (3) the grabbing force (P) at ram connection point, and (4) the force caused by outside of the grapple including the normal pushing force (N2) and the friction force (N2f2).
Two general types of grabbing resistance forces exist while grabbing logs. They are the resistance force caused by logs inside the log grapple and the resistance caused by logs outside the grapple. Since the log grapple usually uses digging motion to grab logs and is sometimes lifted a bit to avoid blocking by logs outside of the grapple, the resistance force caused by logs outside the grapple sometimes might not occur. Furthermore, the model developed is not for computing the actual resistance force but for comparing the relative resistance forces among tong sets. Therefore, the grabbing resistance force caused by logs outside the grapple is not considered in the model. In order to formulate the grabbing resistance (Rr) caused by logs inside the tong and simplify the model, a free log body is considered (Figure 2b). Four different forces are exerted on the log or a bundle of logs under the equilibrium condition. They are the weight of log (Lw.g), the pressure resultant (Pl) from the other logs, the contact force (Nt) from the grapple and the friction force (Ft) of the log sliding along the tong. Since the combined Nt and Ft is the reaction force to the grabbing resistance, Pl and Lw.g are the only forces needed to model the grabbing resistance. The Pl and Lw.g first need to be reflected in a coordinate system of x2oy2 which is a movable system with the log (Figure 2b). The x2-axis is a tangent line to the tong and y2-axis is in the same direction as the normal force at the tangent point. The acted direction of Pl is considered to be horizontal. a is an angle between axes y1 and x and β is the angle between the tangent line of the tong at point (x,y) and the x-axis (Figure 2a). If assume Fr and Nr are the components of Rr on x2-axis and y2-axis respectively, we can have:
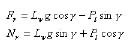 (13)
(13)
Where, Lw
= the mass of log (Kg);
g = acceleration due to gravity
(m/s2);
γ = the angle between the forces
Pl and Nt;
Pl = the pressure resultant from other logs (N);
Let f2 be the friction coefficient between the log and tong. The grabbing resistance Rr for grabbing log can be expressed as:
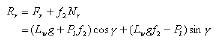 (14)
(14)
According to the additive theorem of trigonometry, if:
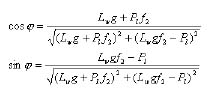 (15)
(15)
then Equation (14) can be expressed as:
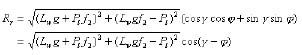 (16)
(16)
Since γ = α + β - 90°, Equation (16) can be further stated as:
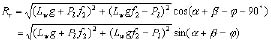 (17)
(17)
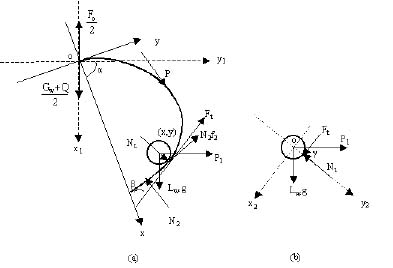
Figure 2. Model of grabbing resistance.
COMPARISONS OF TONG SHAPES
Grabbing Resistance
Under the same grabbing conditions, α and φ are constants in Equation (17) for these three different shapes of tongs. Therefore, the angle of β is the only comparable factor for grabbing resistance in Equation (17). The grabbing resistances are labeled H, C, and V for the tongs of horizontal ellipse, circle and vertical ellipse respectively. Using the mathematical equation of tong shape curve as y = f(x), then,
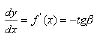 (18)
(18)
Equations (6), (9), and (12) can be denoted as:
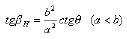 (19)
(19)
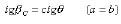 (20)
(20)
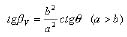 (21)
(21)
Since β ranged from 0 to π/2 and θ is a constant, the following expressions can be derived based on Equations (19), (20), and (21):
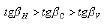 (22)
(22)
β H > β C > β V (23)
Since Pl is usually much greater than Lwg in Equation (15), j must be a very small angle. For the sake of design safety, the forces acted on tongs should be analyzed under a critical condition, which is the tongs are closed and their tips are juxtaposed [5]. Under such a condition, a and β are between p/4and p/2. Therefore, (a + b - j) ranges from p/2 to p and is in the second quadrant (Figure 2a). Since the sine function is decreasing continuously in the second quadrant, we can have:
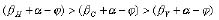 (24)
(24)
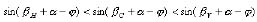 (25)
(25)
Based on Equations (17) and (25), the following expression can be derived:
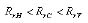 (26)
(26)
Equation (26) indicates that the least grabbing resistance is achieved while grabbing logs with horizontal ellipse tongs. The grabbing resistance also increases from horizontal ellipse tongs, to circular tongs, to vertical ellipse tongs. With the horizontal ellipse tongs, the grapple's height can also be lowered and its stability might be improved as well.
Experimental Analyses
In order to verify the effects of tong shapes on the grabbing performance of a log grapple, three sets of tongs - horizontal ellipse tongs, circular tongs, and vertical ellipse tongs were developed and tested in the Engineering Lab at Northeast Forestry University, Harbin, China. For these three sets of tongs, the open tongs maximum spread and tongs closed area are the same. The geometric parameters are: (1) the long axis of the vertical and horizontal ellipse tongs is 307 mm and the short axis is 280 mm and (2) the radius of the circular tongs is 265 mm (Table 1). Two hydraulic cylinders were used to close or open the tongs and two pulling/pressing sensors were attached to the end of each cylinder for recording the grabbing forces [5].
Table 1. Parameters of the log grapple used in the tests.
| Item |
Value |
|
| Tongs closed area (m2) | 0.22 | |
| Grapple weight (Kg) | 120 | |
| Open tongs max. spread (mm) | 1140 | |
| Grapple height (mm) | ||
| Closed tongs | Horizontal ellipse tongs | 1344 |
| Circular tongs | 1408 | |
| Vertical ellipse tongs | 1474 | |
| Opened tongs | Horizontal ellipse tongs | 1088 |
| Circular tongs | 1168 | |
| Vertical ellipse tongs | 1296 | |
| Grapple width (mm) | 700 | |
| Hydraulic cylinders | ||
| Closing cylinder | Diameter (mm) | 50 |
| Distance of travel (mm) | 280 | |
| Lifting cylinder | Diameter (mm) | 63 |
| |
Distance of travel (mm) |
500 |
Five groups of grabbing tests were conducted for each set of tongs. Log piles were unrestrained. Logs were 2 meters in length and grouped into 4, 8, 12, 16, and 20 cm in scaling diameter groups. Species were Siberian spruce, birch, and some pines. A total of 15 grabs were made for each log diameter class. Since logs were labeled at the ends, their positions in the log pile were about the same for each test. Three variables, grabbing force 1, grabbing force 2, and grabbed log weight, were measured for each test. Two sensors were used to measure grabbing force 1 and 2 respectively and logs were scaled. Average grabbing force was derived by averaging grabbing force 1 and grabbing force 2, and unit grabbing force was obtained by dividing average grabbing force by grabbed log weight. To measure the weight of grabbed logs and grabbing forces, a total of 225 tests were conducted.
An analysis of variance (ANOVA) model was used to determine if any difference existed in the weight of grabbed logs and grabbing force among three sets of tongs and log diameter classes. The ANOVA model can be stated as follows:
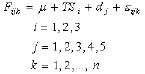 (27)
(27)
Where Fijk represents the kth observation of the grabbing force or the grabbed log weight under the ith set of tongs and the jth log diameter treatment, μ is the mean of each response variable, TSi is the effect of ith tong set, dj is the effect of jth log diameter, eijk is an error component that represents all uncontrolled variability, and n is the number of observations within each treatment.
The grabbed log weight varied from 169.9 Kg with horizontal ellipse tongs to 163.1 Kg with vertical ellipse tongs and was between 126.5 and 217.9 Kg when grabbing logs of 4 to 20 cm diameter classes (Table 2). The grabbed log weight with horizontal ellipse tong differed from the weights with either circular or vertical ellipse tongs (F = 4.15; df = 2,186; P = 0.0173) and was also significantly different among log sizes (F = 259.86; df = 4,186; P = 0.0001). Regardless of log size, the average grabbing forces were 8716.4, 9152.6, and 9555.6 N with horizontal ellipse, circular, and vertical ellipse tongs, respectively. There was a significant difference in the average grabbing force among tong shapes (F = 11.86, df = 2,187; P = 0.0001) and among log sizes (F = 26.71; df = 4,187; P = 0.0001). Correspondingly, the unit grabbing force differed significantly among tong sets (F = 14.33; df = 2,186; P = 0.0001) with average of 52.7, 57.4, and 60.3 N/Kg for horizontal ellipse, circular, and vertical ellipse tongs respectively. The significant difference of the unit grabbing force also existed among log sizes (F = 30.48; df = 4,186; P = 0.0001).
Table 2. Means and significance levels of operational variables for the log grapple1.
| Tong shapes |
Log scaling diameter(cm)4 |
|||||||
| Horizontal ellipse |
Circle |
Vertical ellipse |
4 |
8 |
12 |
16 |
20 |
|
| Grabbed log weight (Kg) | 170a | 165b | 163b | 127d | 145e | 159f | 191g | 218h |
| Grabbing force 1 (N) | 9024a | 9621b | 10180c | 8628d | 8874d | 9664e | 10327f | 10535f |
| Grabbing force 2 (N) | 8409a | 8684ab | 8931b | 7805c | 7998c | 8880d | 9128d | 9649e |
| Average grabbing force2(N) | 8716a | 9153b | 9556c | 8216d | 8436d | 9272e | 9727f | 10093f |
| Unit grabbing force (N/Kg)3 |
52.7a |
57.4b |
60.3c |
65.4d |
58.6e |
58.9e |
51.5f |
46.7g |
1Means with the same letter in a row are not significantly different
at the 5 percent level with Duncan's Multiple-Range Test.
2The average of the
grabbing force 1 and the grabbing force 2.
3The ratio of average grabbing force
and grabbed log weight.
4Values in this part of the table represent the average
for all three tong types at different log sizes.
The grapple with the horizontal ellipse tongs grabbed more logs than the grapple with either circular or vertical ellipse tongs. The grabbed log weight increased with log sizes and ranged from 124.3 Kg for grabbing 4-cm logs with vertical ellipse tongs to 220.4 Kg for grabbing 20-cm logs with horizontal ellipse tongs (Table 3).
Grabbing force is the reaction of grabbing resistance. Regardless of tong shape and log size, the grabbing force increases as the tongs are being closed gradually. The maximum grabbing force was reached when the tongs were closed and the grapple was ready to lift logs. Tong shape and log size significantly affected the grabbing force. The grabbing force increased from horizontal ellipse tongs, to circular tongs, and to vertical ellipse tongs, respectively. It was the lowest at 7901.2 N for grabbing 4-cm logs with horizontal ellipse tongs while it was the highest at 10507.9 N for grabbing 20-cm logs with vertical ellipse tongs.
The unit grabbing force is a combination of average grabbing force and grabbed log weight, and could best describe the grabbing performance of tongs. Consequently, it also varied increasingly from horizontal ellipse tongs, to circular tongs, and to vertical tongs and decreased with log size. It ranged from 44.5 N/Kg for grabbing 20-cm logs with horizontal ellipse tongs to 71.3 N/Kg for grabbing 4-cm logs with vertical ellipse tongs.
CONCLUSIONS
Tong shape significantly affected the grabbing performance of a log grapple. Experimental data verified the theoretical analyses. The grabbing performance of log grapple with horizontal ellipse tongs was better than the grapple with either circular tongs or vertical ellipse tongs while grabbing unrestrained log piles. The least grabbing resistance was achieved while using the horizontal ellipse tongs. The grapple with horizontal ellipse tongs needed to generate relatively smaller grabbing force to grab logs compared to the grapple with either circular or vertical ellipse tongs. Regardless of log size, the grabbing forces of circular and vertical ellipse tongs were 5.0% and 9.6% higher than the 8716.4 N obtained from the horizontal ellipse tongs.
Table 3. Comparisons of the grabbing forces and grabbed log weights.
| Log scaling diameter (cm) |
|||||
| Tong shape | 4 | 8 | 12 | 16 | 20 |
| Average grabbing force (N) |
|||||
| Horizontal ellipse | 7901 | 7911 | 8964 | 9132 | 9778 |
| Circle | 7948 | 8635 | 9394 | 9966 | 10039 |
| Vertical ellipse | 8848 | 8828 | 9502 | 10332 | 10508 |
| Grabbed log weight (Kg) |
|||||
| Horizontal ellipse | 128 | 148 | 165 | 191 | 220 |
| Circle | 127 | 143 | 156 | 193 | 218 |
| Vertical ellipse | 124 | 143 | 157 | 186 | 214 |
| Unit grabbing force (N/Kg) |
|||||
| Horizontal ellipse | 62.8 | 53.7 | 54.9 | 48.1 | 44.5 |
| Circle | 63.3 | 60.8 | 61.4 | 52.1 | 46.6 |
| Vertical ellipse | 71.3 | 62.0 | 60.5 | 56.2 | 49.3 |
The holding capacity of grabbed logs varied decreasingly from horizontal ellipse tongs, to circular, and vertical tongs. The average grabbed log weight of 169.9 Kg with horizontal ellipse tongs was about 3% and 4% higher than the grabbed weights with circular and vertical ellipse tongs respectively.
Accordingly, the unit grabbing force of 52.7 N/Kg with horizontal ellipse tongs was about 9% and 14% lower than the unit forces with circular and vertical ellipse tongs. Therefore, it is concluded that the grapple with approximately horizontal ellipse tongs has better grabbing performance than grapples with circular and vertical ellipse tongs under the grabbing condition on log piles.
Dimensions and specifications of grabbed logs also affected the performance of the log grapple. Within a reasonable range of log sizes, the grabbed log weight and the grabbing force varied increasingly while the unit grabbing force varied decreasingly with log size.
ACKNOWLEDGMENTS
The author would like to thank Mr. Larry Osborn, Dr. Lihai Wang, and Prof. Jiyan Shi for their valuable comments on an earlier draft of this manuscript.
AUTHOR CONTACT
Dr. Jingxin Wang can be contacted by e-mail at --
jxwang@wvu.edu
LITERATURE CITED
[1] Bao, Q. 1984. Introduction to a single rope log grapple. Lifting and Transportation Machines (1): 22-26. [In Chinese].
[2] Cao, Z. 1986. Study on the jaw shape of log grapple. Master Thesis. Northeast Forestry University, Harbin, China. 91 pp.
[3] Fan, Z., Z. Wang, and B. Lu. 1984. Photo elastic experiments with log grapples. For. Sci. 20(4): 61-70. [In Chinese].
[4] Taybep, B. A. 1957. Kinematics of the grabbing mechanism. For. Mach. Institute of Moscow, Publication No. 7, Moscow, Russia.
[5] Wang, J. 1990. Study on the theories of log grapples. Ph.D. Dissertation. Northeast Forestry University, Harbin, China. 311 pp.
[6] Wen, D. 1982. How to increase the holding capability of the grapple. Loading and Unloading in Harbor. (3): 16-20. [In Chinese].