Glen Murphy
New Zealand Forest Research Institute
Rotorua, New Zealand
The author is the South Island Group Leader.
ABSTRACT
An algorithm that combines tabu search principles with a simple improvement- swapping heuristic has been developed for allocating stands and cutting patterns to logging crews for a single time period. A limited set of market and operational constraints has been included. Individual crew productivity has also been taken into account. The algorithm has been implemented in Visual Basic. Tests have been carried out on up to 60 stands, 10 logging crews, and seven cutting patterns. The "best" solutions have usually been found within a few hundred iterations.
Keywords: Forest harvesting, constrained optimisation, tabu search, allocation, value recovery.
INTRODUCTION
Since 1985 there has been a rapid growth in harvest in New Zealand plantation forests, as well as a large increase in the number of domestic and international customers purchasing wood. This in turn has led to a multitude of log types with different specifications and values. As a result, log production management has become increasingly complex and sophisticated. For example, some forest companies have to match markets, logging crews, and forest stands for over fifty log types.
Production planners from most New Zealand forest companies are faced with the task of allocating forest stands and cutting patterns (sets of log types) to logging crews on a weekly basis. The task is complicated by the need to meet operational constraints as well as marketing constraints while at the same time hopefully achieving the best possible return to the forest owner. The allocation process must also allow the "standing down" of a logging crew if that will give the greatest return, i.e., net value recovery.
At this stage it is necessary to digress briefly to define a few of the terms used:
· a stand is an area of trees of uniform composition, silvicultural treatment, and age. There may be more stands available for allocation than there are logging crews.
· a cutting pattern is a subset of log types destined for specific customers from the total set of log types that the forest produces. For example, a simplistic 3 log type cutting pattern might be Domestic Peeler logs (4.9 m) for Customer A, Export Sawlog (8.1 m) for Customer B in Japan, and Domestic Pulp logs (random lengths) for Customer
C. Logging crews in New Zealand usually produce between 10 and 20 different log types. Each logging crew may have a different cutting pattern which is changed often.
· marketing constraints for each log type may include minimum and maximum volume limits, minimum average small-end diameter limits, and minimum and maximum percentage limits for volume for each log type within a log type grouping (e.g., maximum of 5% of volume of all Export Sawlogs to be in short lengths). These are typical constraints faced by many New Zealand forest companies.
· operational constraints for each logging crew may include limitations on the terrain and the tree size in which they could work, their different production rate capabilities, and any loss in production capacity due to time taken up in shifting equipment between stands.
· net value recovery, referred to in this paper, is the financial return the forest owner will get from the sale of the wood once transport costs to the customer and logging crew shifting costs have been deducted. Ideally, it should also have harvesting costs deducted.
A combination of past experience and "what-if" spreadsheets are often used to find "good" solutions to the allocation problem. These solutions can be far from optimal. There are signs that the New Zealand forest industry would welcome a more objective decision-making tool to assist production planners.
Although commercial sensitivity has limited published New Zealand work on the potential improvements, there are some indications that gains could be substantial. In the early 1980s Ferrow and McKewen found that over a third of the potential value of a sample of trees was unrealised by one New Zealand company due to a failure in planning to match cutting patterns with stands and markets [6]. More recently, Cossens (pers. comm.) found that value improvements in the order of 15 to 22% were possible for another New Zealand company.
There are a number of developments underway in New Zealand and overseas that should lead to improvements in revenue from better allocation of stands and cutting patterns to logging crews. This paper describes work carried out at the New Zealand Forest Research Institute in which a computer package incorporating a tabu search heuristic was tested on a series of specifically designed data sets which included all the inputs required for derivation of an optimum solution to the allocation problem for a single time period.
REASONS FOR USE OF A TABU SEARCH HEURISTIC
There are many possible combinations of logging crews, stands, and cutting patterns that need to be evaluated to find the best solution to the forest stand or cutting-pattern allocation problem. While in theory mixed integer programming can be used to formulate these types of problems, in practice they can be very hard to solve in a reasonable time. A number of approaches have resorted to using either a heuristic, an amalgam of heuristics and linear programming, or integer programming. A heuristic is a technique that seeks good (i.e., near-optimal) solutions at a reasonable computational cost without being able to guarantee optimality [17].
Some of the approaches that have been tried but which go only part way to addressing the stand cutting-pattern allocation problem include:
· a binary search procedure that met a single marketing constraint by allocating a cutting pattern to a single stand model for a single time period [16], but which did not consider other operational constraints and the allocation of stands to logging crews;
· a modified Hooke and Jeeves pattern search procedure that incorporated multiple marketing and operational constraints [12], but which was not suitable for multiple stands or the allocation of logging crews to stands;
· an iterative Linear Programming/Dynamic Programming model that allocated cutting patterns to multiple stem classes within a single stand type [5], but which did not consider log type constraints (other than volume) and crew allocation constraints;
· a Goal Programming/Dynamic Programming approach that added log type constraints to a similar type of model as the LP/DP model above for a single stand, but which ignored crew allocation constraints [14];
· a Linear Programming/Dynamic Programming model that generated cutting patterns and log product values to be used in multiple stands for multiple time periods [4]. However, it did not address crew allocation, stand allocation, market constraints (other than volume constraints), operational restrictions on the number of cutting patterns allocated to each crew or the number of log types allocated to each cutting pattern;
· a linear programming planning system that simultaneously selected cutting patterns (from a restricted set) and assigned crews to stands [18, 19] while meeting a limited set of marketing constraints; and
· a mixed integer programming heuristic that allocated logging crews and log types to stands and then conducted a binary search procedure to meet volume, length, and average small-end diameter constraints [15]. Volume matching, not net value recovery maximizing, was the aim during the binary search phase.
A brief search of the published literature and the Internet revealed that tabu search heuristics were being suggested as solutions for a wide range of combinatorial optimization problems [7], including forestry problems in Norway, Chile, USA, and Canada. Glover, one of the earliest developers of tabu search applications, states that tabu search "has achieved impressive practical successes in applications ranging from scheduling and computer channel balancing to cluster analysis and space planning, and more recently has demonstrated its value in treating classical problems such as the travelling salesman and graph coloring problems" [7]. Detailed explanations of tabu search heuristics may be found in Glover [7,8] and Reeves [17].
Tabu search has recently been applied to multiple-period forest harvest scheduling problems with forest-cover spatial constraints [3], wildlife habitat constraints [2], and aquatic habitat constraints [1], and has been suggested as a means for solving forest stand-cutting-pattern allocation problems [10,11, 18].
Laroze developed a tabu search heuristic to find cutting patterns to apply to a single stand to satisfy log-batch average diameter and length distribution market constraints for a single time period [11]. His formulation did not take into account the productivity differences of individual logging crews, nor did it allocate stands to individual crews.
Krcmar-Nozic and others [10] used a tabu search heuristic to allocate logging crews to multiple stands, taking into account machine capability, crew productivity, and environmental impacts. Net present value was maximized over multiple time periods (years). Their approach was aimed at solving a much longer term problem than of interest to the weekly production planner and did not take marketing constraints into consideration.
Since no existing methods fully addressed the production planners problem, and tabu search looked to be a promising solution method, a new model was formulated by the author and a computer program (TABU) was developed.
APPLICATION TO THE STAND ALLOCATION, CREW ALLOCATION, AND CUTTING PATTERN PROBLEM
The TABU program computer code was prepared in VisualBasic and incorporates a simple neighbourhood improvement swapping procedure with the key elements of the tabu search heuristic. The key elements, in general terms, are:
1) constraining the search by classifying certain of its moves (transitions from one solution to another solution) as forbidden (i.e., tabu) for a given number of iterations (the "tabu status").
2) freeing up the search by rules that provide "strategic forgetting" of the tabu status of certain moves. An example of a rule that provides strategic forgetting is that a move's tabu status could be overridden only when the move would result in the "best" solution found up to that point in the search.
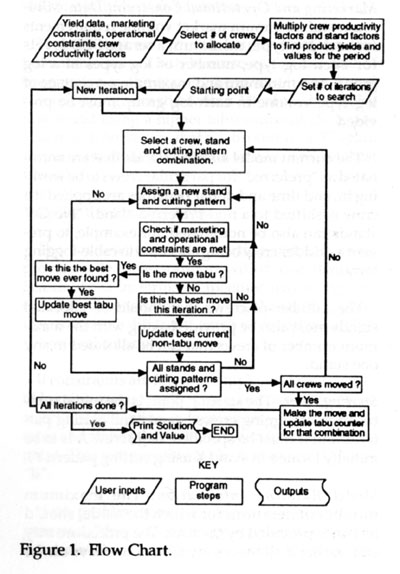
A flow chart of the search procedure is shown in Figure 1. After standardized yield, crew, market, and search parameters are input, the TABU program determines which crew-stand-cutting pattern combination in the current solution to temporarily remove and which new combination to bring into the solution. One combination can only replace another if it meets marketing and operational constraints, does not involve a tabu move, and provides the greatest improvement in value for that iteration (or, in the case of tabu moves, the highest value found in the search so far). Once a combination has moved into the solution it is placed on the tabu list. The neighbourhood swapping procedure continues until the number of iterations specified by the user has been reached or no further feasible solutions can be found. At that stage the best solution is printed out.

Figure 1. Flow Chart.
Inputs
Current inputs to the program are:
Standardized Yield Data: For each stand and cutting pattern, the yield in dollar terms, and for each log type (e.g., Peeler, 12.1 m Export Long, Pulp) in volume terms, must be provided. The average small- end diameter for each log type must also be provided. This information could come from inventory data (adjusted by an experience factor) and an estimate of the number of hectares that could potentially be harvested by a "standard" logging crew from the stand over the period of interest. The length of the period is determined by the user but does not need to be expressly specified.
Crew Productivity Data: A crew name and productivity factor must be provided for each crew. This factor is in relation to a "standard" crew, (e.g., 0.95 of a "standard" crew's production). This information is used to adjust the Standardized Yield Data if the crew is allocated to a particular stand.
Marketing and Operational Constraint Data: Minimum and maximum market volume requirements for each log type, minimum average SED levels for each log type, number of log types in a log group, and minimum and maximum percentage of log type volume in each log group must be provided.
The current model also has stands that are nominated as "preferred" for particular crews to be working in, and time and dollar penalties are applied if a crew is shifted to a non-preferred stand. "No Go" stands can also be nominated, for example, to prevent a skidder crew being allocated to cable-logging terrain.
The number of crews that should be allocated stands must also be provided along with the maximum number of crews that can be allocated to any one stand.
Starting Point: The starting point is the initial combination of logging crews, stands and cutting patterns and it must be specified, (e.g., crew A is to be initially located in stand X using cutting pattern Y).
Model Running Information: The maximum number of iterations for which the model should be run is provided by the user. The procedure may stop earlier if all moves are tabu or no move can be made that meets marketing and operational constraints. The number of moves for which a crew/stand/cutting pattern combination is tabu can be set by the user. Adjusting this value can lead to superior or inferior solutions.
The number of log types, logging crews, stands, and cutting patterns is limited by the available RAM on the computer being used.
Outputs
An example of the output for a 60-stand, 10-crew, 5-cutting-pattern run is shown in Figure 2. It shows the results of the first and thirtieth iterations of the heuristic along with "best" stands and cutting patterns to allocate to each logging crew. Also shown are important statistics for the constrained log types and the dollar value of the best solution found.

Figure 2. Example of output from TABU.
TESTING THE TABU SEARCH HEURISTIC
The heuristic was tested on 10, 25, and 60 stands; on 5 and 10 logging crews; on a maximum of 1, 2, or 5 logging crews per stand; on 5 or 8 cutting patterns; on two methods of starting the search; on five log types; on 3 to 8 constraints; and on a wide range of tabu status values. The heuristic was run for up to 9000 iterations. A comparison was also made with an integer programming (IP) formulation for a small problem. From these tests a number of observations were made.
Comparison with IP Formulation
Two comparisons were made between the TABU heuristic (500 iterations) and an IP formulation for a small problem (10 stands, 5 logging crews, 5 cutting patterns, and 5 log types called data set "A" for future reference). The first test allowed as many logging crews to be located in any one stand as was required. The tabu search solution was within 0.8% of the IP solution. The second test allowed a maximum of one crew per stand. The tabu search solution, found half way through the 500 iterations, was exactly the same as the IP solution.
Rate of Progression Towards an Optimal Solution
The tabu search method moves quickly towards its own "optimal" solution. Figure 3 shows the rate of progression for the second test with the data set "A" referred to above. Within fifty iterations the best solution found was within 1.5% of the optimal solution. Another test with a large data set (60 stands, 10 crews, 5 cutting patterns and 5 log types called data set "B" for future reference) gave after 100 iterations a solution that was within 0.5% of the best solution, which was found after 1400 iterations (optimal solution not known).
Varying the TABU Status
Glover suggests that a procedure using multiple runs with different lengths of tabu restriction is useful to follow when using tabu search methods [7]. If the tabu status is too small the search may cycle around a local optimum and if it is too large "pathways" to better local optima may be missed.
For example, for data set "A" it was found that, for a tabu status up to 23, the search cycled around a local optimum and the best value found (not the local optimum creating the cycling) was within 1.5% of the true optimum. A tabu status of 27 found the optimum solution and a tabu status of 29 found a solution that was within 0.06% of the optimum. A tabu status of 57 quickly constrained and stopped the search although the best solution found was still within 1.5% of the optimum.
Tests on data set "B" also found cycling on low tabu status values but, because of the fast rate of progression in the search, the best solution found before cycling was still within 1% of the best solution found using a higher tabu status of 29. It was also noted, however, that a tabu status of 37 again resulted in cycling (solution within 0.6% of best found).
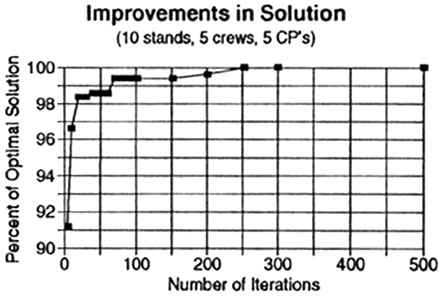
Figure 3. Rate of progression towards an optimal solution for a small data set ("A") using the TABU search heuristic.
Varying the Starting Point
The heuristic requires a starting point that will provide a feasible solution within one iteration. Feasibility is in terms of meeting marketing and operational constraints. Varying the starting point may result in a different search path and possibly a better final solution.
If constraints are few and simple, and the number of logging crews small, it may be possible to easily select a combination of logging crews, cutting patterns and stands that will provide a feasible starting point. This was possible for both data sets "A" and "B".
If the problem is more complex one option is to generate a "dummy" starting point that meets all the constraints but is made up of cutting patterns with large negative values for a randomly selected set of stands. The tabu search procedure will then quickly move to a real feasible starting point if one can be found. The dummy starting point method was used successfully for both data set "A" and a medium sized data set (25 stands, 10 logging crews, 7 cutting patterns, 5 log types called data set "C" for future reference). The tabu search procedure found a solution that was within 0.6% of the optimal using a dummy starting point for data set "A". For data set "C" a user-selected starting point yielded a "best" solution that was 0.2% less than that found using a dummy starting point.
Constraint "Tightness" and Complexity
The number of feasible solutions found at each iteration, from which the current best is selected, will be determined by the number and "tightness" of the constraints. If the constraints are too restrictive no feasible solution (other than a dummy solution) may be found. For example, the tabu search heuristic was unable to find a feasible first solution for a real-world data set of 25 stands, 10 logging crews, 5 cutting patterns, and 29 log types where there were minimum and maximum volume constraints on all 29 of the log types until a number of the volume constraints were relaxed.
For another data set with 25 stands, 10 logging crews, 7 cutting patterns, 5 log types, and 8 constraints the heuristic had little difficulty in finding good solutions.
Solution Accuracy Versus Data Accuracy
Forest inventories in Australian and New Zealand plantation forests aim for a probable (p = 0.05) limit of error (PLE) of less than 10% for total stand volume. This results in a PLE of less than 5% for total stand value (M. Lawrence, pers. comm.). The combined value from 20 stands, each with a PLE of 5%, would have an overall PLE of about 1.25%. A maximum solution error of 0.8% was found for the single data set ("A") for which a comparison could be made between the tabu search optimum and the IP theoretical optimum. If this is typical of larger problems then the errors associated with the data inputs are at best of the same order and at worst one or two orders of magnitude greater than the difference between the best tabu search optimum and the theoretical optimum.
Time Taken to Reach an Optimum Solution
The solution time was approximately linearly related to the product of number of iterations with number of stands with number of logging crews with number of log types with number of cutting patterns. For example, 500 iterations of data set "A" (500*10*5*5*5 = 625,000) would take about the same amount of time to run (approximately 10 minutes on a 80 mhz 486DX CPU) as 42 iterations of data set "C" (42*60*10*5*5 = 630,000).
WHERE TO FROM HERE?
The TABU computer program described in this paper can be used in its current form to allocate stands and cutting patterns to logging crews. It is currently being evaluated by two New Zealand forest companies. Further refinements are planned to improve its usefulness. These include:
1) Modification of the algorithm to allow faster solution times and to limit the internal cycling that can be triggered by low tabu status values.
2) Use of extreme value theory to estimate the difference between the TABU optimum and the maximum likely value that could be obtained.
3) Automation of procedures for managing constraints (i.e., by relaxing lower priority constraints or by cascading excess volume from one log type to lower value log types).
4) Extension of the program to include multiple time periods.
Further research is needed to determine the number of cutting patterns considered to be realistic in practice, and to define good cutting patterns that are easily implemented.
REFERENCES
[1] Bettinger, P. 1996. Spatial analysis techniques for ensuring the compatibility of land management activities and aquatic habitat goals in Eastern Oregon. Ph.D. Dissertation. Oregon State University, Corvallis, Oregon.
[Return to text]
[2] Boston, K. 1996. Using tabu search to solve tactical forest planning problems with spatial wildlife habitat goals and constraints. Ph.D. Dissertation. Oregon State University, Corvallis, Oregon.
[Return to text]
[3] Brumelle, S., D. Granot, M. Halme, and I. Vertinsky. 1996. A tabu search algorithm for finding a good forest harvest schedule satisfying green-up constraints. Working Paper. FEPA, UBC, Vancouver, BC.
[Return to text]
[4] Cossens, G.P. 1996. Optimisation of log allocation. M.App.Sc. Thesis, Lincoln University, New Zealand. 124 pp.
[Return to text]
[5] Eng, G., H.G. Dallenbach, and A.G.D. Whyte. 1986. Bucking tree-length stems optimally. Canadian Journal of Forest Research 16:10301035.
[Return to text]
[6] Ferrow, G. and B.J. McKewen. 1980. The determination of the profit sacrificed in felling, extraction and log allocation processes. Report of an investigation submitted in partial fulfilment of the requirements of the Degree of Bachelor of Management Studies of the University of Waikato, Hamilton, New Zealand. 91 pp. (Unpublished).
[Return to text]
[7] Glover, F. 1989a. Tabu Search Part I. ORSA Journal in Computing 1(3):190206.
[Return to text]
[7] Glover, F. 1989a. Tabu Search Part I. ORSA Journal in Computing 1(3):190206.
[Return to text]
[7] Glover, F. 1989a. Tabu Search Part I. ORSA Journal in Computing 1(3):190206.
[Return to text]
[7] Glover, F. 1989a. Tabu Search Part I. ORSA Journal in Computing 1(3):190206.
[Return to text]
[8] Glover, F. 1989b. Tabu Search Part II. ORSA Journal in Computing 2(1):4-32.
[Return to text]
[9] Glover, F. and M. Laguna. 1993. Tabu search. In: Reeves, E.R. (ed.). Modern Heuristic Techniques for Combinatorial Problems. J. Wiley & Sons, New York. Pp. 70150.
[Return to text]
[10] Krcmar-Nozic, E., G.C. van Kooten, I. Vertinsky, and S. Brumelle. 1996. Economic and environmental impacts of harvesting methods in forest planning. Forest Economics and Policy Analysis Research Unit, University of British Columbia, Vancouver, BC. 25 pp.
[Return to text]
[10] Krcmar-Nozic, E., G.C. van Kooten, I. Vertinsky, and S. Brumelle. 1996. Economic and environmental impacts of harvesting methods in forest planning. Forest Economics and Policy Analysis Research Unit, University of British Columbia, Vancouver, BC. 25 pp.
[Return to text]
[11] Laroze, A. 1993. Development and comparison of stand level bucking optimisation. Masters Thesis. Oregon State University, Corvallis, Oregon.
[Return to text]
[11] Laroze, A. 1993. Development and comparison of stand level bucking optimisation. Masters Thesis. Oregon State University, Corvallis, Oregon.
[Return to text]
[12] Murphy, G. 1993. Optimising value recovery under constrained market and operational conditions. Paper presented at International Symposium on Systems Analysis and Management Decisions in Forestry, Valdivia, Chile, March 9-12, 1993. 12 pp.
[Return to text]
[13] Murphy, G., D. Lane, and P. Cossens. 1996. Progress report on the development of an integrated value management system. In: Proceedings of the Annual Council on Forest Engineering Meeting, Marquette, Michigan, July 1996. Pp 124-9.
[Return to text]
[14] Nasberg, M. 1985. Mathematical programming models for optimal log bucking. Linkoping University, Dissertation No. 132. 200 pp.
[Return to text]
[15] Ogweno, D.C.O. 1994. Integrated optimisation of operational and tactical planning of log production. Ph.D. Thesis. School of Forestry, University of Canterbury, New Zealand. 177 pp.
[Return to text]
[16] Sessions, J. , E. Olsen, and J. Garland. 1989. Tree bucking for optimal stand value with log allocation constraints. Forest Science 35:271-6.
[Return to text]
[17] Reeves, C.R. 1993. Modern heuristic techniques for combinatorial problems. J. Wiley and Sons, New York. 320 pp.
[Return to text]
[17] Reeves, C.R. 1993. Modern heuristic techniques for combinatorial problems. J. Wiley and Sons, New York. 320 pp.
[Return to text]
[18] Weintraub, A., R. Morales, J. Seron, R. Epstein, and P. Traverso. 1991. Managing operations in pine forest industries. Proceedings of the 1991 Symposium on Systems Analysis in Forest Resources. USDA Forest Service, Southeastern Forest Experiment Station, General Technical Report SE-74. Pp. 31-34.
[Return to text]
[18] Weintraub, A., R. Morales, J. Seron, R. Epstein, and P. Traverso. 1991. Managing operations in pine forest industries. Proceedings of the 1991 Symposium on Systems Analysis in Forest Resources. USDA Forest Service, Southeastern Forest Experiment Station, General Technical Report SE-74. Pp. 31-34.
[Return to text]
[19] Weintraub, A. 1995. Planning packages: will the computer do it all? Proceedings of LIRO Harvest Planning Seminar, Nelson, New Zealand.
[Return to text]